Filling the hyperbolic plane with triangles
As part of his senior capstone project, our outstanding graduate Cliff Taylor studied hyperbolic geometry and wrote a computer program to illustrate tessellations of the hyperbolic plane by triangles. In addition to creating many compelling images, Cliff also uncovered some beautiful and mysterious mathematical ideas.
Many of you will remember how to tessellate the Euclidean plane with a triangle.

One way to create this image is to begin with a single triangle,

and reflect it across one of its edges to create a second triangle.
Continuing in this way, the entire tessellation will be created.
Hyperbolic geometry involves looking inside a disk and using a notion of distance that differs from our usual Euclidean notion. In the hyperbolic plane, the shortest path between two points is given by the portion of a circular arc passing through the two points. To create his tessellations, Cliff began with a triangle in the hyperbolic plane, like this:
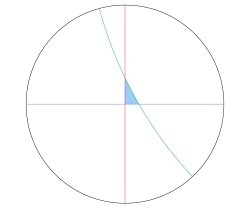
He the reflected it across its sides
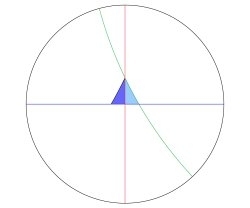
and continued:
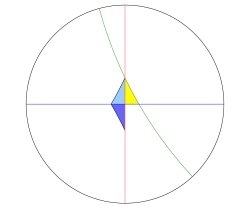
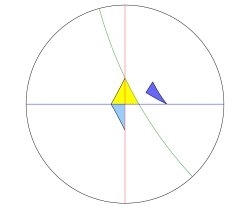
Without some care, this procedure will double back on itself so that reflecting one triangle creates another we've already encountered. We would then be stuck in a cycle, creating a sequence of triangles over and over and never creating more.
Fortunately, there is a rather sophisticated theory, developed using recently uncovered ideas in geometry and the theory of computation, that provides a way around this problem. Cliff learned about this theory as a part of his project and used it to implement his computer program.
Here is a gallery of some of the images that Cliff constructed.







