Suppose you have a certain number of cans of the same radius. What's the smallest square box that you could put them in without putting one can on top of another? This kind of question fascinates mathematicians: it's easy to ask, but answering it requires serious thought.

One of the mathematicians searching for answers is Grand Valley faculty member Will Dickinson, who worked on similar questions as an undergraduate with Bob Conley at Cornell University. On a recent sabbatical in the fall of 2006, Will and his family spent the semester at Cornell where Will renewed his research in this area, known as equal circle packings, and constructed an impressive computer program, called EZ Pack, to investigate them.

Based on his own undergraduate experience, Will felt this would be an ideal research area in which to engage undergraduates. During the summer REU program at Grand Valley in 2007, Will worked on these questions with Daniel Guillot, from Louisana State University, and Ashley Castelaz, from the University of North Carolina, Asheville. Last summer, Will worked with Grand Valley student Sandi Xhumari in the Summer Student Scholars program. Together, they have found some interesting results that have earned widespread attention and praise. 

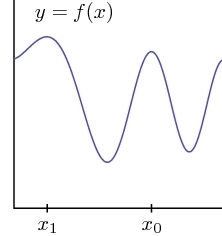
To describe their results, recall the notion of local maxima from your calculus course. When studying a function f(x), a point x₀ is a local maximum if the function cannot be made larger by making small changes in x. A local maximum is not necessarily a global maximum, a point at which the function cannot be made larger, even with large changes in x. The graph to the left has a global maximum at x₁.

Now imagine that you have n circles of equal radius and you would like to place them in a box, such as shown at the top of the page. The goal is to make the ratio of the area of the circles to the area of the square as large as possible. Mathematicians refer to this ratio as the density of the configuration. If we think about the size of the square being fixed, we would like to find configurations in which the radius of the circles is as large as possible.

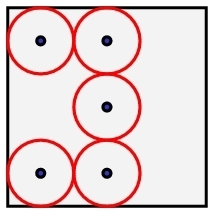
If you look at the configuration on the right, you may believe that we could move the centers of the circles around to allow us to increase their radii and hence the density of the configuration. This configuration is not a local maximum for the density. 

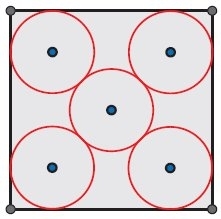
Starting from the next configuration shown on the right, however, it is not possible to move the centers of the circles in such a way that the radii may be increased. For this reason, this configuration is a local maximum of the density. It is, however, not a global maximum. 

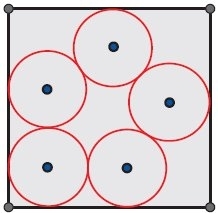
The configuration shown on the right has a higher density. In fact, with some work, one can prove that there is no configuration with a higher density; this one is the global maximum. 

Rather than working with a square, Will and his collaborators considered equal circle packings on the torus, which may be thought of as the surface of a bagel. Anyone who has played the classic 80's video game Asteroids is familiar with the geometry of a torus. When your ship flies off the top of the screen, it reappears at the bottom. Or when it flies off the right side of the screen, it reappears on the left. To a mathematician, this simply means thinking of the top and bottom of the screen as the same line segment and thinking of the left and right as the same. (To obtain the bagel, imagine rolling the square so that the top and bottom touch one another. This produces a cylinder. Now bend the cylinder so that the two edges of the cylinder touch and you've got a bagel. Yummy.)

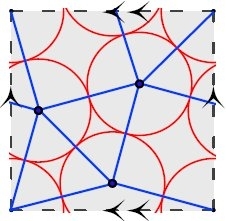
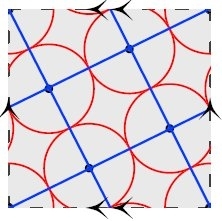
Working with his students, Will found that some questions about circle packings on the torus required different techniques than those used on an ordinary square. For instance, on the torus, they were able to make a finite list of possible "packing graphs" (the collection of blue line segments between tangent circles shown above) that could lead to locally maximally dense packings. This allowed the team to identify the configurations above as the global maxima when four or five circles are packed on a torus and to prove that any configuration of five or fewer circles that is a local maximum of the density is also a global maximum.

Will and his students have presented their findings at several national conferences, where they have attracted considerable attention. Perhaps most impressively, a short article about this work appeared in Science. In that article, the well-known mathematician Ronald Graham, of the University of California at San Diego, said, "It is very difficult to prove that a particular packing is optimal." Working on the torus, where there is no boundary, may make certain proofs easier to find, he continues.

You may enjoy experimenting with equal circle packings using the software that Will created on his sabbatical. It is freely available at the EZ Pack website.