Did you know that The Mackinac Gazette's logo is a proof of the Pythagorean theorem?

You'll remember that the Pythagorean theorem gives a relationship between the lengths of the legs of a right triangle and the length of the hypotenuse. More specifically, the squares of the lengths of the legs add to the square of the length of the hypotenuse.

Another way of stating the Pythagorean theorem is to construct squares on each of the sides of the triangle. The theorem then says that the area of the blue square added to the area of the green square gives the area of the gray square.

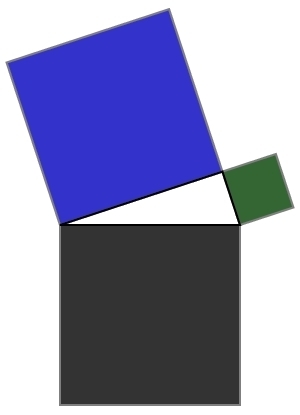
To form our logo, we simply shift the blue square

and repeat the pattern formed by the blue and green squares (the gray square is no longer drawn):

We now add the outlines of the gray squares back in

and shift these squares so that they pass through the centers of the blue squares to produce our logo. Notice that each gray square contains a green square and four quarters of a blue square. Therefore, the area of a gray square equals the areas of a green square and a blue square, which is precisely what the Pythagorean theorem says.

The Pythagorean theorem is extremely old: a Babylonian tablet, dated to approximately 1000 B.C., contains a statement of the theorem. It is not known if Pythagoras, who lived in the sixth century B.C., found a proof of the theorem, but Euclid's Elements, written about two hundred years after Pythagoras, contains two proofs.

If you need to see more proofs, you may read 77 more here. In 1928, Elisha Loomis published The Pythagorean Proposition (reprinted in 1968 by the National Council of Teachers of Mathematics), which contains 365 different proofs! Perhaps we will soon see a desk calendar, one proof for each day, for sale.

Can you name a notable accomplishment of President James Garfield's administration? Neither could our editorial staff. Garfield, elected president in 1880, was assassinated after serving less than four months of his term. However, while serving in the House of Representatives, Garfield found a novel proof of the Pythagorean theorem, given as proof #5 in the link above.