The largest known prime number, 2^57,885,161 - 1, was discovered on January 25, 2013 after a search involving a great deal of computer time spread across many computers.

So how large is this number? Big. Really big. It has 17,425,170 digits, four times as many digits as the number that was previously the largest known prime. If you were to print this number in 12 point font, it would go on for 30 miles. If you wanted to download it in a computer file, it would take up 22.5 megabytes. You could include it in a Gmail message but just barely. It's a big number.

You probably remember that prime numbers are integers that are larger than 1 and divisible only by themselves and 1. If you wanted to create a list, it would begin 2, 3, 5, 7, 11, 13, 17, and so forth. In fact, your list would never end; over two thousand years ago, Euclid proved that there are infinitely many primes.

Our newest known prime is an example of a Mersenne prime, named after the 17th century French monk, Marin Mersenne, who made an extensive study of them. Mersenne primes are prime numbers that have the form 2ⁿ - 1. If you create a list of the numbers 2ⁿ - 1, it would start like this:

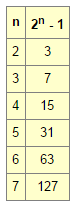
Judging from this short list, you might think that 2ⁿ - 1 is prime whenever n itself is prime. In fact, it's pretty easy to see that 2ⁿ - 1 is not prime if n is not prime. However, 2¹¹ - 1 = 2047 = 23 * 89, which shows that 2ⁿ - 1 is not necessarily prime when n is prime.

While we do know that there are infinitely many Mersenne primes, at this time we only know 48 of them! They seem to be pretty scarce.

So why should we be interested in this latest prime? One reason is that prime numbers form the backbone of many encryption algorithms. For instance, when you place an order online, your credit card number is encrypted using a "key" created by multiplying two large prime numbers. To decrypt the credit card number, an online criminal must determine the key's two prime factors. The security of your transaction relies on the fact that it is much harder to factor a large number into primes than it is to multiply two primes. Which task would you prefer: multiply 127 * 8191 or factor 1,040,257? To ensure the continued security of these encryption algorithms, we would like to have an increasingly large supply of prime numbers with which to create keys.

A second reason involves the means by which this prime number was discovered. The Great Internet Mersenne Prime Search (GIMPS) is a project that utilizes the underused resources of thousands of computers around the world in its search for prime numbers. You may join this project by downloading a program from https://www.mersenne.org/. During your lunch hour, while you're trying to decide whether to play that black seven on the red eight, your computer will happily be crunching away in cooperation with thousands of other computers worldwide. The fact that this computation can be broken up into smaller pieces and handed off to thousands of different computers is a significant feat of computation.

A third reason? Well, it's just kind of cool. Humans have known about prime numbers for a very long time. We've known that there are infinitely many for several thousand years. Yet we are still finding new ones, and there are still a great many questions about prime numbers whose answers we don't know.

Mathematics seeks to uncover eternal truths. However, there will eternally be new truths waiting to be uncovered.